Finding the Jamming Limit

We first look at Weiner's elementary approach to finding the jamming limit $C_R$ (see ¹). Using our previously derived master equation Weiner solved for $M(x)$ recursively, giving us the following results:

$$ \begin{equation} M(x) = \begin{dcases} 0 & \text{if } x \in [0, 1) \\ 1 & \text{if } x \in [1, 2) \\ 3 - \frac{2}{x - 1} & \text{if } x \in [2, 3) \\ 7 - \frac{10 - 4 \ln(x - 2)}{x - 1} & \text{if } x \in [3, 4) \end{dcases} \end{equation} $$

$$ \begin{array} {|c|c|} \hline x & M(x) / x \\ \hline 0.99 & 0 \\ 1.99 & 0.5025125628 \\ 2.99 & 0.6672156769 \\ 3.99 & 0.6854478541 \\ 4.99 & 0.6969110964 \\ 5.99 & 0.7054612992 \\ 6.99 & 0.7114892709 \\ \hline \end{array} $$

and so on - the calculations becoming increasingly difficult, and frankly tedious, after this point. In table we have calculated $M(x) / x$ for values of $x$ close to the upper limit of each interval. As can be seen, the values of $M(x) / x$ seem to be approaching a limit. This can be seen more clearly in the following figure:

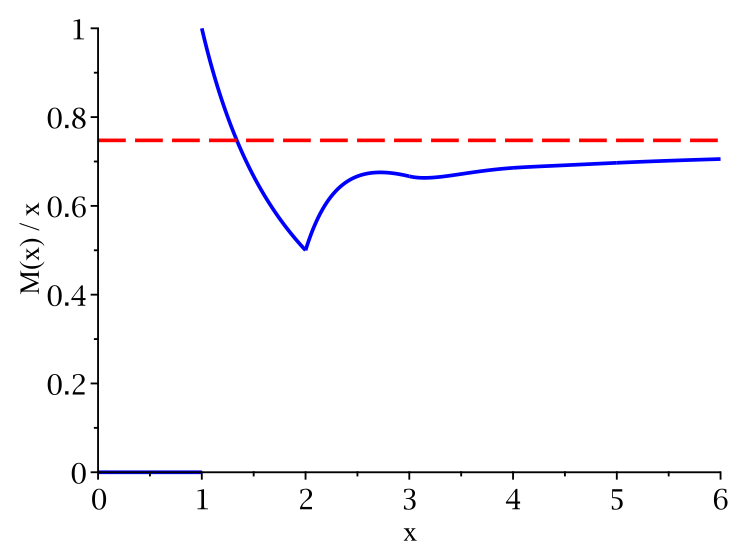
Existence of the Jamming Limit

In attempting to show that this jamming limit exists, Weiner took a flawed approach. In order to understand the flaw we trace his steps and return to equation. Dividing across by $x$ we get:

$$ \begin{equation} \frac{M(x + 1)}{x} = \frac{1}{x} + \frac{2}{x^2} \int_{0}^{x} M(t) dt \end{equation} $$

differentiating with respect to $x$:

$$ \left(\frac{M(x + 1)}{x}\right)^{\prime} = -\frac{1}{x^2} - \frac{4}{x^3} \int_{0}^{x} M(t) dt + \frac{2}{x^2} M(x) $$

looking at the integral, and making use of the fact that $0 \leq M(x) \leq x$ we find that:

$$ \begin{align*} \int_{0}^{x} M(t) dt & \leq \int_{0}^{x} t dt \\ & \leq \frac{x^2}{2} \end{align*} $$

making use of both we find:

$$ \begin{align*} \left(\frac{M(x + 1)}{x}\right)^{\prime} & = -\frac{1}{x^2} - \frac{4}{x^3} \int_{0}^{x} M(t) dt + \frac{2}{x^2} M(x) \\ & \leq -\frac{1}{x^2} - \frac{4}{x^3} \cdot \frac{x^2}{2} + \frac{2}{x^2} \cdot x \\ & \leq -\frac{1}{x^2} - \frac{2}{x} + \frac{2}{x} \\ & \leq -\frac{1}{x^2} \\ & = \mathcal{O}\left(\frac{1}{x^2}\right) \end{align*} $$

and hence:

$$ \lim_{x \to \infty} \left(\frac{M(x + 1)}{x}\right)^{\prime} = 0 $$

which according to Weiner implies that:

$$ \lim_{x \to \infty} \frac{M(x)}{x} = C_R $$

this, however, is incorrect, as a simple counterexample will demonstrate. We consider:

$$ \begin{align*} f(x) & = \sin(\ln(x)) \\\ f^{\prime}(x) & = \frac{\cos(\ln(x))}{x} \\\ \lim_{x \to \infty} f^{\prime}(x) & = \lim_{x \to \infty} \frac{\cos(\ln(x))}{x} \\\ & = 0 \end{align*} $$

but clearly:

$$ \begin{align*} \lim_{x \to \infty} \sin(\ln(x)) & = [-1, 1] \\ & \neq \text{a constant} \end{align*} $$

so this is an unsatisfactory justification for the existence of the limit. Of course if his approach had been to show that:

$$ \left( \lim_{x \to \infty} \frac{M(x + 1)}{x}\right)^{\prime} = 0 $$

his conclusions would have been correct. However, the limit of the derivative of a function is not always the same as the derivative of the limit of a function. As both derivatives (and integrals) are themselves limits, the issue here is if the respective limits are independent. As both the limit, and the integration, are over $x$, then this presents a problem.

Bounds for the Jamming Limit

Weiner did not calculate the limit, but instead provided a method for finding increasingly narrower bounds for the limit. Let us assume for now that:

$$ \lim_{x \to \infty} \frac{M(x)}{x} = C_R $$

in order to find bounds for $C_R$ Weiner sought to sandwich $M(x)$ between two linear functions:

$$ \begin{equation} L_{a_1}(x) \leq M(x) \leq L_{a_2}(x) \end{equation} $$

and find the limits of each of these linear functions as $x \to \infty$. Weiner found an initial lower bound by finding, for $x \geq 1$, the linear function of the form $L(x) = ax + b$ that satisfied the following equation:

$$ \begin{align*} L(x + 1) & = 1 + \frac{2}{x} \int_{1}^{x} L(t) dt \\ ax + (a + b) & = 1 + \frac{2}{x} \int_{1}^{x} (at + b) dt \\ ax + (a + b) & = 1 + \frac{2}{x} \left[ \frac{at^2}{2} + bt \right]_{t = 1}^{x} \\ ax + (a + b) & = 1 + ax + 2b - \frac{a + 2b}{x} \\ (a + b) & = 1 + 2b - \frac{a + 2b}{x} \\ (a + b)x & = x + 2bx - ( a + 2b ) \\ (b - a + 1)x & = a + 2b \end{align*} $$

noting that both sides of the equation must equal $0$, we arrive at two simultaneous equations:

$$ \begin{align*} a - b & = 1 \\ a + 2b & = 0 \end{align*} $$

from which we find the coefficients of our required linear function:

$$ L(x) = \frac{2}{3}x - \frac{1}{3} $$

We know that:

$$ L(x) \leq M(x) = 1 \quad \text{for } 1 \leq x < 2 $$

as $M(x)$ is increasing, we see that, for $x \geq 1$:

$$ \frac{L(x)}{x} \leq \frac{M(x)}{x} $$

and hence:

$$ \lim_{x \to \infty} \frac{L(x)}{x} \leq \lim_{x \to \infty} \frac{M(x)}{x} $$

which gives us:

$$ \frac{2}{3} \leq C_R $$

Weiner went on to find two linear functions that sandwiched $M(x)$ with a little more accuracy. The two functions found were:

$$ \begin{align*} L_{a_1}(x) & \equiv 0.7432x - 0.2568 \\ L_{a_2}(x) & \equiv 0.75x - 0.25 \end{align*} $$

with the property found in the equation $3$:

$$ 0.7432x - 0.2568 \leq M(x) \leq 0.75x - 0.25 $$

dividing across by $x$ and taking the limit as $x \to \infty$:

$$ 0.7432 \leq C_R \leq 0.75 $$

which gives a reasonably good indication of the bounds of $C_R$.

Remarks

Weiner made use of the following theorem and lemma (both stated without proof):

to justify his result.

While Weiner's approach is interesting from the point of view of it's elementary nature, it is not a particularly satisfying approach due to the error made in his justification of the existence of the limit, and also because of the "trial-and-error method" used to find the bounds.

But while his assumption about the existence of the limit is flawed, he does provide an interesting, albeit dated, approach to finding the limit. His work has little more than novelty value, and is included in the survey because of it's historical interest - to see how the understanding of the problem has progressed.